EOQ-Modell: Klassischer Ansatz zur Bestandsoptimierung

Das Wilson-Modell, auch klassische Losformel oder EOQ (Economic Order Quantity) genannt, ist eine mathematische Methode, um zu berechnen, wie oft und in welcher Menge bei einem Lieferanten bestellt werden sollte, um so ein ordnungsgemäßes Bestandsmanagement zu gewährleisten. Das Modell ist ein klassischer Ansatz, der zwar mittlerweile von weniger statischen Methoden abgelöst wurde, jedoch nach wie vor zum Basis-Wissen über Lieferketten gehört.

Das EOQ-Modell wird normalerweise mit der Beschaffung von Rohstoffen und einem optimalen Bestandsmanagement in Verbindung gebracht, jedoch ist zu berücksichtigen, dass dieses Modell tatsächlich auf jede Art von Waren angewendet werden kann.

Formel des EOQ-Modells

Ursprünglich wurde die Formel bereits im Jahre 1913 vom amerikanischen Ingenieur Ford Whitman Harris entwickelt. Doch erst 1934 gelang es dem Berater R. H. Wilson, die Formel erfolgreich auszuarbeiten. Wie sieht die Wilson-Formel denn nun aus?

Basierend auf der Nachfrage nach einem Produkt, den Kosten für die Auftragsabwicklung und den Kosten für die Lagerung wird in der Formel das optimale Auftragsvolumen angegeben. Die mathematische Gleichung lautet wie folgt:

• Q= optimale Bestellmenge
• D= jährliche Nachfrage nach dem entsprechenden Rohstoff
• K= Kosten für die Abwicklung eines Auftrags
• G= Kosten für die Lagerung einer Einheit im Lager innerhalb einer bestimmten Zeitspanne

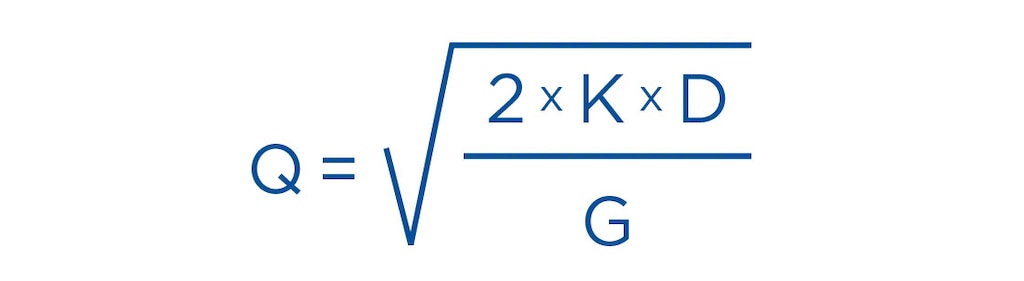
Anwendungen und Einschränkungen

Dieses mathematische Modell zielt darauf ab, das Bestellvolumen für jedes erforderliche Produkt zu optimieren und anzugeben, wann und in welcher Menge bei einem Lieferanten bestellt werden soll.

Mit diesen Daten kann auch der Zeitpunkt der Bestellung festgelegt werden, wobei die Lead Time und der Sicherheitsbestand berücksichtigt werden. Das Wilson-Modell hat jedoch gewisse Einschränkungen und wurde aus diesem Grund mittlerweile von moderneren Ansätzen abgelöst. Diese mathematische Lösung ist nur auf Unternehmen anwendbar, bei denen die beiden folgenden Annahmen erfüllt sind:

• Das Unternehmen hat das ganze Jahr über eine konstante Nachfrage nach Rohstoffen.
• Das zu erwerbende Produkt hat zeitlose Fixkosten, wobei im Laufe des Jahres keine großen Preisschwankungen auftreten.

Wenn z. B. die Kosten des Rohstoffs je nach Saison variieren, lässt sich diese mathematische Formel nicht mehr anwenden, da diese Variable nicht berücksichtigt wird.

Folglich ist diese Methode nur auf bestimmte Unternehmen anwendbar, bei denen Nachfrage und Kosten während des gesamten Jahres nicht stark schwanken.

Vorteile des Modells

Für Unternehmen, die beide der oben genannten Bedingungen erfüllen, ermöglicht diese mathematische Berechnungsmethode eine Optimierung der Bestandsverwaltung. Diese Lösung bietet folgende Vorteile:

• Reduzierung der Kosten für Beschaffung und Lagerung.
• Vermeidung von Überbeständen bei gleichzeitiger Sicherstellung, dass jederzeit genügend Vorräte vorhanden sind, um die Nachfrage zu decken.
• Erfassung des für jede Bestellung korrekten Kaufbetrags.
• Vermeidung von Out-of-Stock-Situationen.

Praktisches Beispiel für das Wilson-Modell

Die fiktive Firma Orch Kork produziert und vertreibt Korken für Weinfirmen in der Region. Um seine Jahresproduktion von 10.000 Einheiten zu decken, kauft das Unternehmen über das ganze Jahr 1.000 kg Rinde der Korkeiche.

Wenn jede Bestellung 200 Euro, einschließlich Transportkosten, kostet und die Kosten für die Lagerung des Produkts 2.000 Euro pro Jahr betragen, was ist dann das optimale Bestellvolumen?

In diesem Beispiel ergibt sich Q (die optimale Bestellmenge) aus der Quadratwurzel der folgenden Formel: √((2*200*1000)/2000). Das Ergebnis der Gleichung ist 14,14.

In diesem Fall beträgt die optimale Menge pro Bestellung also 14 kg. Das bedeutet, dass Orch Kork über das Jahr verteilt Bestellungen über 14 kg Korkeichenrinde aufgeben sollte um über die optimale Menge an Rinde für die Korkproduktion zu verfügen und gleichzeitig eine zu lange Lagerung des Rohmaterials sowie mögliche Out-of-Stock-Situationen zu vermeiden. In diesem Beispiel müsste das Unternehmen also innerhalb eines Jahres 71 Bestellungen über 14 kg Rinde aufgeben, um seinen Jahresbedarf von 1.000 kg Korkeichenrinde zu decken.

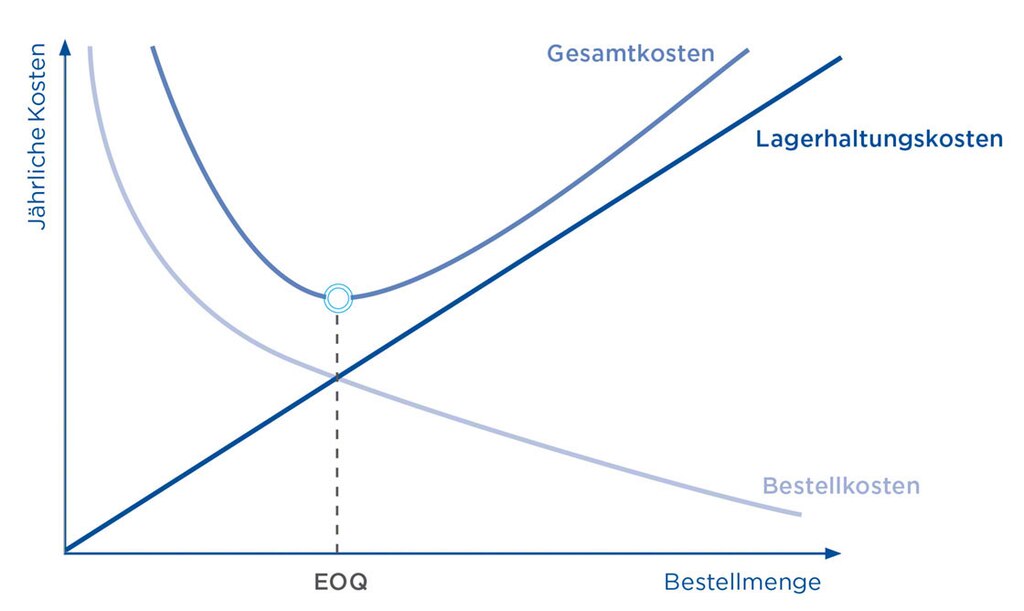
EOQ: Bestandskosten minimieren, wenn es keine Saisonabhängigkeit gibt

Durch die Anwendung des Wilson-Modells bei der Bestandsverwaltung können das Bestellvolumen optimiert und damit die Gesamtkosten für Lagerung und Einkauf minimiert werden. Das Modell ist jedoch nur dann anwendbar, wenn Nachfrage und Preise das ganze Jahr über konstant sind. In komplexeren Situationen ist das Modell nicht mehr anwendbar, sodass in diesem Fall ein Lagerverwaltungssystem die bessere Lösung darstellt.